Fast Kalman Filtering with univariate treatment Part I---Basics
June 1, 2018 | Michael GongFast Kalman Filtering with univariate treatment Part I—Basics
1. Introduction
1.1 Classic Gaussian Kalman Filter
In the standard multivariate linear state space model, the measurement vector $y_t$ depends linearly on the unobserved state vector $\alpha_t$. If we assume the Gaussian distribution of the measurement and state disturbanceds, the signal extraction can be done using classic Gaussian Kalman Filter. However, when the dimension of the measurement vector $y_t$, or its dimension is time-varying, the signal extraction is usually infeasible or unstable since we need to invert the measurement covariance at each Kalman recursion. To avoid the measurement covariance inversion, Koopman and Durbin (2000, Journal of Time Series Analysis) proposed a fast filtering technique called univariate treatment. In the first part of this series, I will present the problem and give a quick implementation of the Kalman Filtering with univariate treatment.
I follow the syntax of Koopman and Durbin, the general state space model can be defined as
$$y_{t} = Z f_{t} + \epsilon_{t} \quad \epsilon_{t} \sim N(0,H) $$ $$f_{t} = d + T f_{t-1} + \eta_{t} \quad \eta_{t} \sim N(0,Q) $$
then the latent factor $f_t$ can be evaluated recursively by the Kalman Filter algorithm:
$$v_t = y_t -Z f_t , \quad F_t = ZP_tZ’ + H$$ $$f_{t|t} = f_t + P_tZ’F_t^{-1}v_t, \quad f_{t+1} = T f_{t|t} + d$$ $$P_{t|t} = P_t - P_tZ’F_t^{-1}ZP_t, \quad P_{t+1} = TP_{t|t}T’ + Q$$
The problem of the classic Kalman Filter is that we need to invert the covariance matrix $F_t$ at each time step. If the dimension of $y_t$ is high, the inversion of a big matrix is slow and numerically unstable.
1.2 Univariate Treatment
The basic idea of univariate treatment is to introduce the elements of the measurements one at a time into the filtering and smoothing process. We can write univariate representation of the measurement equation as follow:
$$ y_{j,t} = Z_{j,t}f_{t} + \epsilon_{j,t} \quad \text{for} \quad j = 1, …, N_t, \ t = 1, …., T$$
where $j$ is the observation index, and $N_t$ is the dimension of $y_t$. The Kalman filtering and predicting of the univariate representation can be computed recursively:
$$ f_{j+1,t} = f_{j,t} + K_{j,t}v_{j,t}, \quad P_{j+1,t} = P_{j,t} - K_{j,t}F_{j,t}K^{‘}_{j,t}$$ $$ f_{j,t+1} = d+ T f_{N_{t+1},t}, \quad P_{1, t+1} = T P_{N_{t+1},t}T’ +Q $$
where $P_{t}$ is the conditional variance of $f_{t}$, $\sigma^2_{j,t}$ is the squared $j$th diagonal element of $H_{t}$, and
$$ v_{j,t} = y_{j,t} - Z_{j,t}f_{j,t}, \quad F_{j,t} = Z_{j,t}P_{j,t}Z’P_{j,t} + \sigma^2_{j,t}, \quad K_{j,t} = P_{j,t}Z’_{j,t}F^{-1}_{j,t}$$
The univariate recursion algorithm makes factor extraction and estimation feasible because the prediction error $v_{j,t}$ and the measurement covariance $F_{j,t}$ are two scalars, which avoid big matrix inversion ($F^{-1}_{j,t}$) in the classic Kalman recursion.
2. Quick Python Implementation
Let’s take a look of how to implement the Kalman Filtering with univariate treatment
def UniFilter(a1, p1, Z, H, vD, mT, mQ, Y, sizes):
'''
a1: initial state mean
p1: initial state variance
Z: measurement loading, 3d numpy array
H: measurement disturbance covariance, 3d numpy array
vD: vector of state constant
mT: transition matrix
mQ: state disturbance matrix
Y: 3d numpy array of measurements
sizes: dimension of Y at each time t
'''
r = a1.shape[0]
N, M = Y.shape[0], Y.shape[1]
# allocate memory and initialize
aF = np.zeros((r, N), dtype=np.float64)
pF = np.zeros((N, r, r), dtype=np.float64)
aP = np.zeros((r, N + 1), dtype=np.float64)
pP = np.zeros((N + 1, r, r), dtype=np.float64)
aP[:, 0] = a1.ravel().copy()
pP[0] = p1.copy()
a = a1
p = p1
v = np.zeros((M, N), dtype=np.float64)
F = np.zeros((M, N), dtype=np.float64)
K = np.zeros((N, r, M), dtype=np.float64)
# Time filtering
for i in range(N):
mY, mZ, mH = Y[i].ravel(), Z[i], H[i].ravel()
m = sizes[i]
# Observation filtering
for j in range(m):
mZp = mZ[j, :]
v[j, i] = mY[j] - np.dot(mZp, a)
F[j, i] = mZp @p @mZp.T + mH[j]
K[i][:, j] = ((p @mZp.T) / F[j, i]).ravel()
if F[j, i] > 0:
a = a + K[i][:, j] * v[j, i]
p = p - F[j, i] * np.outer(K[i][:, j],K[i][:, j])
aF[:, i] = a.ravel()
pF[i] = p
a = mT @a + vD
p = mT @p @mT.T + mQ
aP[:, i+1] = a.ravel()
pP[i+1] = p
return aF, pF, aP[:, 1:], pP[1:]Let’s generate some data and test the univariate filter
def genStates(vD, mT, mQ, N):
eta = np.random.multivariate_normal(vD, mQ, [N])
f = np.zeros_like(eta)
for i in range(1,N-1):
f[i+1] = vD + mT@f[i] + eta[i]
return f
def genMeasure(mZ, mH, f):
N = f.shape[0]
M = mZ.shape[0]
y = np.zeros([M, N])
eps = np.random.multivariate_normal(np.zeros(M), mH, [N])
y = np.zeros_like(eps).T
for i in range(1, N-1):
y[:,i] = mZ@f[i] + eps[i]
return y
N = 200
r = 4
m = 10
mZ = np.random.rand(m,r)
mH = np.diag(np.random.normal(0,1,m)**2)
vD = np.zeros(4)
mT = np.eye(r) * 0.97
mQ = np.random.normal(0,1,[r,r])
mQ = mQ.T@mQ
f = genStates(vD,mT,mQ,N)
y = genMeasure(mZ,mH,f)Prepare the data such that they fit the dimension requirement
a1 = np.zeros(r)
p1 = np.eye(r)
Z = np.zeros([N,m,r])
H = np.zeros([N,m,m])
Y = np.zeros([N,m,1])
for i in range(N):
Z[i], H[i],Y[i] = mZ,mH,y[:,[i]]
sizes = np.ones(N,dtype=np.int32)*r
# Filtering
aF,pF,aP,pP = UniFilter(a1, p1, Z, H, vD, mT, mQ, Y, sizes)Let’s plot the filtered states against the true (simulated) states
fig = plt.figure(figsize=(12,10))
for i in range(r):
ax = fig.add_subplot(2,2,i+1)
ax.plot(aF[i,:], label=f"filtered state")
ax.plot(f[:,i], label=f"True state")
ax.set_title(f"{i+1}th factor")
plt.legend()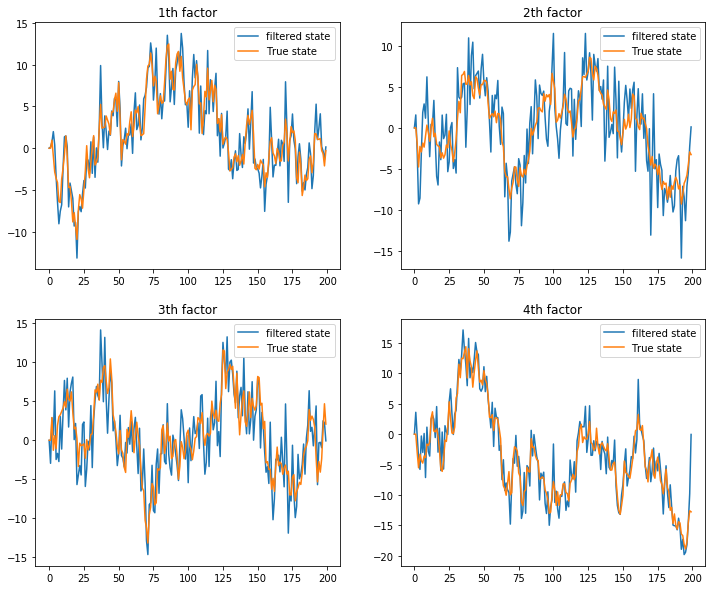
We see that the univariate filter successfully extract the true states from the nosiy measurement
3. Problem of current implementaion
We see that the univariate filter implemented in pure Python/Numpy environment successfully extract the true factors. However, since Python is a interpreted language, if the time seires is too long or the state dimension is too large, the pure Python loop would be very time consuming! Below the standard Kalman Filtering, let’s compare the performance!
def KalmanFilter(a1, p1, mZ, mH, vD, mT, mQ, mY):
m = mY.shape[0]
N = mY.shape[1]
r = a1.shape[0]
a = a1.copy()
P = p1.copy()
aF = np.zeros([N, r, 1])
pF = np.zeros([N, r, r])
aP = np.zeros([N, r, 1])
pP = np.zeros([N, r, r])
F = np.zeros([N, m, m])
v = np.zeros([N, m, 1])
K = np.zeros([N, r, m])
L = np.zeros([N, r, r])
for i in range(0, N):
v[i] = mY[:, [i]] - mZ@a
F[i] = mZ@P@mZ.T + mH
invF = np.linalg.inv(F[i])
K[i] = mT@P@mZ.T@invF
aF[i] = a + P@mZ.T@invF@v[i]
pF[i] = P - P@mZ.T@invF@mZ@P
aP[i] = mT@a + vD
pP[i] = mT@P@mT.T + mQ
return aF, pF, aP, pPTime the filtering time-elapse
%timeit aF, pF, aP, pP = KalmanFilter(a1[:,None],p1,mZ,mH,vD[:,None],mT,mQ,y)12.6 ms ± 312 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)%timeit aF, pF, aP, pP = UniFilter(a1, p1, Z, H, vD, mT, mQ, Y, sizes)18.8 ms ± 205 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)As we see, the univariate filter actually runs slower than the standard filter! In the Part II of this series, we will turn to C++ implementation to truely utilize the advantage of univariate filter!