Python Tutorial Part II--Numpy and Pandas
April 3, 2017 | Michael Gong1. Numpy/Scipy
NumPy and SciPy are open-source add-on modules to Python that provide common mathematical and numerical routines in pre-compiled, fast functions. These are growing into highly mature packages that provide functionality that meets, or perhaps exceeds, that associated with common commercial software like MatLab.
The NumPy (Numeric Python) package provides basic routines for manipulating large arrays and matrices of numeric data.
The SciPy (Scientific Python) package extends the functionality of NumPy with a substantial collection of useful algorithms, like minimization, Fourier transformation, regression, and other applied mathematical techniques.
import numpy as np Matlab to Numpy translation click here
Numpy Complete documentation click here
Scipy Complete documentation click here
print(np.__version__)
np.__config__.show()1.11.2
openblas_lapack_info:
NOT AVAILABLE
blas_mkl_info:
libraries = ['mkl_intel_lp64', 'mkl_intel_thread', 'mkl_core', 'iomp5', 'pthread']
include_dirs = ['/home/michael/anaconda3/include']
define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
library_dirs = ['/home/michael/anaconda3/lib']
lapack_mkl_info:
libraries = ['mkl_intel_lp64', 'mkl_intel_thread', 'mkl_core', 'iomp5', 'pthread']
include_dirs = ['/home/michael/anaconda3/include']
define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
library_dirs = ['/home/michael/anaconda3/lib']
blas_opt_info:
libraries = ['mkl_intel_lp64', 'mkl_intel_thread', 'mkl_core', 'iomp5', 'pthread']
include_dirs = ['/home/michael/anaconda3/include']
define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
library_dirs = ['/home/michael/anaconda3/lib']
lapack_opt_info:
libraries = ['mkl_intel_lp64', 'mkl_intel_thread', 'mkl_core', 'iomp5', 'pthread']
include_dirs = ['/home/michael/anaconda3/include']
define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
library_dirs = ['/home/michael/anaconda3/lib']1.1 Array creation
a = np.array([1,2,3])
print(type(a))
print(a)<class 'numpy.ndarray'>
[1 2 3]b = np.array([[1,2,3],[3,4,5]])
print("this is b\n",b)
print("the shape of b is:",b.shape)
print("the dimension of b is:",b.ndim)
print("number of elements of b:", b.size)this is b
[[1 2 3]
[3 4 5]]
the shape of b is: (2, 3)
the dimension of b is: 2
number of elements of b: 6** A little bit introduction of object oriented programming**
a = np.array([1,2,3,3,4,5,5,6,7])
print("the type of a:",type(a))
b = a.reshape(3,3)
print("the type of b:",type(b))
c1 = b**2
print("the type of c:",type(c1))
# we can write:
c2 = np.array([1,2,3,3,4,5,5,6,7]).reshape(3,3)**2
print(np.allclose(c1,c2))the type of a: <class 'numpy.ndarray'>
the type of b: <class 'numpy.ndarray'>
the type of c: <class 'numpy.ndarray'>
True1.2 Array operation
# generate random ndarray
mA = np.random.randint(1,10,size=(3,3))
mB = np.random.randint(1,10,size=(3,3))
vC = np.random.randint(1,10,size=(3,1))
vD = np.random.randint(1,10,size=(1,3))
print("mA:\n",mA)
print("mB:\n",mB)
print("vC:\n",vC)
print("vD:\n",vD)mA:
[[8 9 6]
[1 3 7]
[5 3 2]]
mB:
[[6 7 1]
[3 2 4]
[5 8 2]]
vC:
[[9]
[1]
[2]]
vD:
[[3 6 8]]element-wise operation *,/,+,-
print(mA+mB)[[14 16 7]
[ 4 5 11]
[10 11 4]]print(mA-mB)[[ 2 2 5]
[-2 1 3]
[ 0 -5 0]]print(mA/mB)[[ 1.33333333 1.28571429 6. ]
[ 0.33333333 1.5 1.75 ]
[ 1. 0.375 1. ]]print(mA*mB)[[48 63 6]
[ 3 6 28]
[25 24 4]]print(mA-vC)[[-1 0 -3]
[ 0 2 6]
[ 3 1 0]]print(mA-vD)[[ 5 3 -2]
[-2 -3 -1]
[ 2 -3 -6]]print(mA*mB-vC + mB**2)[[ 75 103 -2]
[ 11 9 43]
[ 48 86 6]]Matrix operation
Matrix mupliplication @
# The matrix multiplication is done by @ operation (in python 3.0+), in python 2.*, it is done by "dot" method
print(mA@mB)[[105 122 56]
[ 50 69 27]
[ 49 57 21]]Matrix transpose T
print(mA.T)[[8 1 5]
[9 3 3]
[6 7 2]]Matrix inversion “inv”
print(np.linalg.inv(mA))
# to make it easier to type, we import the "inv" function alone
from numpy.linalg import inv
print(inv(mA))[[ -1.42857143e-01 6.93889390e-18 4.28571429e-01]
[ 3.14285714e-01 -1.33333333e-01 -4.76190476e-01]
[ -1.14285714e-01 2.00000000e-01 1.42857143e-01]]
[[ -1.42857143e-01 6.93889390e-18 4.28571429e-01]
[ 3.14285714e-01 -1.33333333e-01 -4.76190476e-01]
[ -1.14285714e-01 2.00000000e-01 1.42857143e-01]]# again, we can benefit from the OOP design
ret = mA.T@inv(mB) - vC + mB.T@vC - vD
print(ret)[[ 57.5 53.89285714 47.46428571]
[ 80. 75.28571429 69.42857143]
[ 12.75 9.23214286 7.16071429]]1.3 Slicing
A = np.random.rand(3,3)
print(A)
print(A[:,[0]])[[ 0.07731399 0.10377817 0.1793915 ]
[ 0.84609483 0.65710391 0.17246314]
[ 0.7439164 0.89687702 0.1211748 ]]
[[ 0.07731399]
[ 0.84609483]
[ 0.7439164 ]]# slicing is done through bracket []
print(mA)
print('the first element is:\n',mA[0,0])
print('the first column is:\n',mA[:,[0]])
print('the first two columns are:\n',mA[:,:2])
# boolean and integer indexing
indexB = np.array([True, False, True])
indexI = np.array([1,0,1])
array = np.array([1,2,3])
print("Boolean indexing result:\n" ,array[indexB])
print("Integer indexing result:\n", array[indexI])[[8 9 6]
[1 3 7]
[5 3 2]]
the first element is:
8
the first column is:
[[8]
[1]
[5]]
the first two columns are:
[[8 9]
[1 3]
[5 3]]
Boolean indexing result:
[1 3]
Integer indexing result:
[2 1 2]1.4 Frequently used Numpy function
- diag: create diagonal matrix from vector
- diagonal: extract the diagonal element
- eye: identity matrix
- zeros: matrix filled with zero
- ones: matrix filled with one
- reshape: reshape the matrix
vY = np.random.rand(3)
print(vY.shape,type(vY))(3,) <class 'numpy.ndarray'>print(np.diag(vY))[[ 0.36944492 0. 0. ]
[ 0. 0.46322172 0. ]
[ 0. 0. 0.80256682]]print(np.diagonal(np.diag(vY)))[ 0.36944492 0.46322172 0.80256682]print(np.eye(3))[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]print(np.zeros([3,3]))
print(np.ones([3,3]))[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]print(np.zeros_like(vY))
print(np.zeros_like(np.diag(vY)))[ 0. 0. 0.]
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]# benefits of the OOS design
print((np.diag(vY)+np.random.rand(3,3)).reshape(9,1).max()**2)1.386368103441.5 Some example and exercises
(1) Subtract the mean of each row of a matrix
a = np.random.rand(3,3)
b = a - a.mean(axis=1) #np.mean(a,axis=1)
print(b)[[-0.27371758 -0.13738752 0.631215 ]
[-0.25698583 -0.11128908 0.68699173]
[-0.30855162 0.03770426 -0.26797938]](2) compute the moving average of an array
def moving_average(vY,window):
T = vY.shape[0]
ret = np.zeros(T - window)
for j,t in enumerate(range(window,T)):
ret[j] = vY[t-window:t].mean()
return ret
vY = np.random.rand(20)
window = 5
ret = moving_average(vY,window)
print(ret)[ 0.31439101 0.3067207 0.2612112 0.4488305 0.51791912 0.40021872
0.5155174 0.60879213 0.60470478 0.58250843 0.57880459 0.60341439
0.62814638 0.6328429 0.73670997](3) find the closest point
def find_closePointV1(points,target):
min_distance = 1
point_index = 0
for i,point in enumerate(points):
distance = ((point-target)**2).sum()
if distance < min_distance:
min_distance = distance
point_index = i
return min_distance,point_index
def find_closePointV2(points,target):
distances = ((points-target)**2).sum(axis=1)
min_distance = distances.min()
point_index = distances.argmin()
return min_distance,point_indexpoints = np.random.rand(2000,2)
target = np.array([0.5,0.5])
min_distance1,point_index1 = find_closePointV1(points,target)
min_distance2,point_index2 = find_closePointV2(points,target)
print("Version 1 the minimum distance:",min_distance1)
print("Version 1 the point with minimum distance",points[point_index1])
print("Version 2 the minimum distance:",min_distance2)
print("Version 2 the point with minimum distance",points[point_index2])Version 1 the minimum distance: 0.000113540004683
Version 1 the point with minimum distance [ 0.50663792 0.50833535]
Version 2 the minimum distance: 0.000113540004683
Version 2 the point with minimum distance [ 0.50663792 0.50833535]# version 1 and version 2 have huge performance difference
%timeit find_closePointV1(points,target)100 loops, best of 3: 5.76 ms per loop%timeit find_closePointV2(points,target)The slowest run took 4.57 times longer than the fastest. This could mean that an intermediate result is being cached.
10000 loops, best of 3: 46.9 µs per loop(4) One line code of simulation of Pi
N = 1000000
pi = 4*((np.random.rand(N,2)**2).sum(axis=1)<1).sum()/N
print(pi)3.1411642. Pandas
Pandas is an open source, BSD-licensed library providing high-performance, easy-to-use data structures and data analysis tools for the Python programming language.
- Use Pandas as possible as you can!
import pandas as pd2.1 ** Object creation**
index = [i for i in range(4)]
columns = ['A','B','C','D','E']
data = pd.DataFrame(np.random.rand(4,5),index=index,columns=columns)
print(data) A B C D E
0 0.377511 0.935913 0.484039 0.494305 0.017102
1 0.674354 0.961497 0.719836 0.463993 0.966345
2 0.113718 0.558731 0.725746 0.287497 0.447674
3 0.799740 0.051104 0.585415 0.475480 0.6512202.2 ** Selction**
data['A']0 0.582853
1 0.205175
2 0.142668
3 0.517169
Name: A, dtype: float64data[['A','B']]| A | B | |
|---|---|---|
| 0 | 0.582853 | 0.050482 |
| 1 | 0.205175 | 0.676394 |
| 2 | 0.142668 | 0.728272 |
| 3 | 0.517169 | 0.224242 |
data[0:3]| A | B | C | D | E | |
|---|---|---|---|---|---|
| 0 | 0.582853 | 0.050482 | 0.257578 | 0.340971 | 0.907032 |
| 1 | 0.205175 | 0.676394 | 0.830756 | 0.963753 | 0.675394 |
| 2 | 0.142668 | 0.728272 | 0.353043 | 0.082804 | 0.585398 |
# Label based selection
data.loc[3,'B']0.22424205926919127data.loc[0:2,['A','B']]| A | B | |
|---|---|---|
| 0 | 0.582853 | 0.050482 |
| 1 | 0.205175 | 0.676394 |
| 2 | 0.142668 | 0.728272 |
# integer based selection
data.iloc[1:4,0:2]| A | B | |
|---|---|---|
| 1 | 0.205175 | 0.676394 |
| 2 | 0.142668 | 0.728272 |
| 3 | 0.517169 | 0.224242 |
data.iloc[1:3,:]| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0.205175 | 0.676394 | 0.830756 | 0.963753 | 0.675394 |
| 2 | 0.142668 | 0.728272 | 0.353043 | 0.082804 | 0.585398 |
data.ix[1:3]| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0.205175 | 0.676394 | 0.830756 | 0.963753 | 0.675394 |
| 2 | 0.142668 | 0.728272 | 0.353043 | 0.082804 | 0.585398 |
| 3 | 0.517169 | 0.224242 | 0.585978 | 0.654013 | 0.965902 |
# Boolean indexing
indexB = data['A'] > 0.2
print(indexB)
print(data[indexB])0 True
1 True
2 False
3 True
Name: A, dtype: bool
A B C D E
0 0.582853 0.050482 0.257578 0.340971 0.907032
1 0.205175 0.676394 0.830756 0.963753 0.675394
3 0.517169 0.224242 0.585978 0.654013 0.965902# or conveniently
print(data[data['A']>0.2]) A B C D E
0 0.582853 0.050482 0.257578 0.340971 0.907032
1 0.205175 0.676394 0.830756 0.963753 0.675394
3 0.517169 0.224242 0.585978 0.654013 0.965902# OOP
data[data['A']>0.2]['C'].ix[0]0.257577504604104222.3 Arithmatic operations
data['F'] = (data['A'] + data['B'])/data['C'] - data['D']*data['E']
print(data) A B C D E F
0 0.772780 0.251506 0.638696 0.712863 0.639697 1.147697
1 0.723921 0.383294 0.007697 0.661608 0.638037 143.427074
2 0.808509 0.679512 0.296928 0.872748 0.898736 4.227009
3 0.226408 0.768940 0.292466 0.896504 0.974840 2.5293432.4 Apply
def func(series):
return series.sum()/series.std()
ret = data.apply(func,axis=1)
data['ret'] = data.apply(func,axis=1)
print(ret)
print('\n')
print(data)0 5.779099
1 2.757361
2 6.135847
3 5.855379
dtype: float64
A B C D E F ret
0 0.772780 0.251506 0.638696 0.712863 0.639697 1.147697 5.779099
1 0.723921 0.383294 0.007697 0.661608 0.638037 143.427074 2.757361
2 0.808509 0.679512 0.296928 0.872748 0.898736 4.227009 6.135847
3 0.226408 0.768940 0.292466 0.896504 0.974840 2.529343 5.8553792.5 Groupby
This is a extremely useful object, please go through the detail cookbook
By “group by” we are referring to a process involving one or more of the following steps
- Splitting the data into groups based on some criteria
- Applying a function to each group independently
- Combining the results into a data structure
data = pd.DataFrame({'A' : ['foo', 'bar', 'foo', 'bar',
'foo', 'bar', 'foo', 'foo'],
'B' : ['one', 'one', 'two', 'three',
'two', 'two', 'one', 'three'],
'C' : np.random.randn(8),
'D' : np.random.randn(8)})
data| A | B | C | D | |
|---|---|---|---|---|
| 0 | foo | one | 0.785 | -0.553 |
| 1 | bar | one | 0.724 | 1.079 |
| 2 | foo | two | -1.760 | -0.818 |
| 3 | bar | three | 0.721 | 0.440 |
| 4 | foo | two | 0.026 | 0.068 |
| 5 | bar | two | 0.442 | 0.321 |
| 6 | foo | one | -0.328 | 0.176 |
| 7 | foo | three | -0.473 | -1.483 |
groupA = data.groupby('A')
groupAB = data.groupby(['A','B'])
print(groupA)
print(groupAB)<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7eff7ff467b8>
<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7eff7ff46128># GroupBy object attributes
groupA.groups{'bar': Int64Index([1, 3, 5], dtype='int64'),
'foo': Int64Index([0, 2, 4, 6, 7], dtype='int64')}# some statistics
# Std
print(groupAB.std())
# Mean
print(groupAB.mean())
# Sum
print(groupAB.sum()) C D
A B
bar one NaN NaN
three NaN NaN
two NaN NaN
foo one 0.287689 0.533024
three NaN NaN
two 0.259739 0.182370
C D
A B
bar one 0.093289 -1.435398
three 1.610691 0.099456
two 1.674365 -1.969331
foo one -0.433944 0.118717
three 0.640498 0.695818
two 1.002847 -0.708532
C D
A B
bar one 0.093289 -1.435398
three 1.610691 0.099456
two 1.674365 -1.969331
foo one -0.867888 0.237433
three 0.640498 0.695818
two 2.005694 -1.417063Iteration through groups
for group_name, group_data in groupA:
print('group name: ',group_name)
print('group data:\n',group_data)
print('\n')group name: bar
group data:
A B C D
1 bar one -1.763415 -1.015387
3 bar three -1.104977 -2.578075
5 bar two -1.650251 -0.601321
group name: foo
group data:
A B C D
0 foo one 0.738800 0.320824
2 foo two -0.866414 -0.223506
4 foo two 0.009047 -0.798006
6 foo one 0.209088 -0.120664
7 foo three -0.470803 0.823928# you can flexibly run function on group data, for example: OLS regression
beta = np.zeros(2)
for i, (group_name,group_data) in enumerate(groupA):
mY = group_data[['C']].values
mX = group_data[['D']].values
beta[i] = np.linalg.lstsq(mX,mY)[0]
print(beta)[ 0.7005281 0.00695643]# the method above is very flexible, you can use another useful method: group apply
def myfunc(group_data):
print(group_data)
mY = group_data[['C']].values
mX = group_data[['D']].values
return np.linalg.lstsq(mX,mY)[0]
groupA.apply(myfunc) B C D
1 one -1.763415 -1.015387
3 three -1.104977 -2.578075
5 two -1.650251 -0.601321
B C D
1 one -1.763415 -1.015387
3 three -1.104977 -2.578075
5 two -1.650251 -0.601321
B C D
0 one 0.738800 0.320824
2 two -0.866414 -0.223506
4 two 0.009047 -0.798006
6 one 0.209088 -0.120664
7 three -0.470803 0.823928
A
bar [[0.700528102717]]
foo [[0.00695642969842]]
dtype: objectdef myfunc(group_data):
mY = group_data[['C']].values
mX = group_data[['D']].values
return float(np.linalg.lstsq(mX,mY)[0])
result = groupA.apply(myfunc)
print(result)A
bar 0.700528
foo 0.006956
dtype: float64def myfunc(group_data):
# if the return result is a dataframe, pandas will look at its index, and merge the result back to original
# dataframe by same index
return (group_data['C']/group_data['D'].sum()).to_frame('ret')
data['ret'] = data.groupby('A').apply(myfunc)
data| A | B | C | D | ret | |
|---|---|---|---|---|---|
| 0 | foo | one | -0.230517 | -0.258188 | 0.476460 |
| 1 | bar | one | 0.093289 | -1.435398 | -0.028224 |
| 2 | foo | two | 1.186510 | -0.579577 | -2.452417 |
| 3 | bar | three | 1.610691 | 0.099456 | -0.487309 |
| 4 | foo | two | 0.819184 | -0.837487 | -1.693185 |
| 5 | bar | two | 1.674365 | -1.969331 | -0.506574 |
| 6 | foo | one | -0.637371 | 0.495621 | 1.317392 |
| 7 | foo | three | 0.640498 | 0.695818 | -1.323855 |
2.6 Merge data
This is another power object, please go through detail
basic syntax:
pd.merge(left, right, how='inner', on=None, left_on=None, right_on=None,
left_index=False, right_index=False, sort=True,
suffixes=('_x', '_y'), copy=True, indicator=False)left = pd.DataFrame({'key': ['K0', 'K1', 'K2', 'K3'],
'A': ['A0', 'A1', 'A2', 'A3'],
'B': ['B0', 'B1', 'B2', 'B3']})
right = pd.DataFrame({'key': ['K1', 'K2', 'K3', 'K4'],
'C': ['C0', 'C1', 'C2', 'C3'],
'D': ['D0', 'D1', 'D2', 'D3']})
print(left)
print(right) A B key
0 A0 B0 K0
1 A1 B1 K1
2 A2 B2 K2
3 A3 B3 K3
C D key
0 C0 D0 K1
1 C1 D1 K2
2 C2 D2 K3
3 C3 D3 K4inner_merged = pd.merge(left,right,how='inner',left_on=['key'],right_on=['key'])
print(inner_merged) A B key C D
0 A1 B1 K1 C0 D0
1 A2 B2 K2 C1 D1
2 A3 B3 K3 C2 D2left_merged = pd.merge(left,right,how='left',left_on=['key'],right_on=['key'])
print(left_merged) A B key C D
0 A0 B0 K0 NaN NaN
1 A1 B1 K1 C0 D0
2 A2 B2 K2 C1 D1
3 A3 B3 K3 C2 D22.7 Pivot and reshape table
…Again…very power object, details click here
data = pd.DataFrame({'A' : ['foo', 'bar', 'foo', 'bar',
'foo', 'bar', 'foo', 'foo'],
'B' : ['one', 'one', 'two', 'three',
'two', 'two', 'one', 'three'],
'C' : np.random.randn(8),
'D' : np.random.randn(8)})
data| A | B | C | D | |
|---|---|---|---|---|
| 0 | foo | one | 1.329326 | 0.515690 |
| 1 | bar | one | 0.912863 | -0.309627 |
| 2 | foo | two | -0.219018 | 2.094762 |
| 3 | bar | three | -0.159688 | 0.737186 |
| 4 | foo | two | 1.182747 | 0.359100 |
| 5 | bar | two | -0.013464 | -1.514432 |
| 6 | foo | one | -1.277657 | 0.657462 |
| 7 | foo | three | 0.012385 | 0.535246 |
table = pd.pivot_table(data,index=['A'],columns=['B'],values=['C'])
print(table) C
B one three two
A
bar 0.912863 -0.159688 -0.013464
foo 0.025835 0.012385 0.4818652.7 Useful funciton on DataFrame
data.describe()data.describe(percentiles=[0.2,0.3,0.4,0.8])# shape
data.shape# transpose
data.T# link to numpy
data_values = data.values
print(type(data_values))
print(data_values)# caveat, data_values is a "VIEW" of the DataFrame, which means that it is mutable!
data_values[0,0] = 15
data3. Learn Pandas by example
import matplotlib.pyplot as plt
%matplotlib inline
data = pd.read_csv('data.csv')
data.head(6)| Date | minor | Open | High | Low | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2010-01-04 | AAPL | 213.430 | 214.500 | 212.380 | 214.010 | 123432400.000 | 27.727 |
| 1 | 2010-01-04 | INTC | 20.790 | 21.030 | 20.730 | 20.880 | 47800900.000 | 16.443 |
| 2 | 2010-01-04 | MSFT | 30.620 | 31.100 | 30.590 | 30.950 | 38409100.000 | 25.555 |
| 3 | 2010-01-05 | AAPL | 214.600 | 215.590 | 213.250 | 214.380 | 150476200.000 | 27.775 |
| 4 | 2010-01-05 | INTC | 20.940 | 20.990 | 20.600 | 20.870 | 52357700.000 | 16.435 |
| 5 | 2010-01-05 | MSFT | 30.850 | 31.100 | 30.640 | 30.960 | 49749600.000 | 25.564 |
data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 5412 entries, 0 to 5411
Data columns (total 8 columns):
Date 5412 non-null object
minor 5412 non-null object
Open 5412 non-null float64
High 5412 non-null float64
Low 5412 non-null float64
Close 5412 non-null float64
Volume 5412 non-null float64
Adj Close 5412 non-null float64
dtypes: float64(6), object(2)
memory usage: 338.3+ KB# change the column name
data.rename(columns={'minor':'ticker'},inplace=True)
data.head(5)| Date | ticker | Open | High | Low | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2010-01-04 | AAPL | 213.430 | 214.500 | 212.380 | 214.010 | 123432400.000 | 27.727 |
| 1 | 2010-01-04 | INTC | 20.790 | 21.030 | 20.730 | 20.880 | 47800900.000 | 16.443 |
| 2 | 2010-01-04 | MSFT | 30.620 | 31.100 | 30.590 | 30.950 | 38409100.000 | 25.555 |
| 3 | 2010-01-05 | AAPL | 214.600 | 215.590 | 213.250 | 214.380 | 150476200.000 | 27.775 |
| 4 | 2010-01-05 | INTC | 20.940 | 20.990 | 20.600 | 20.870 | 52357700.000 | 16.435 |
data.sort_values(by=['ticker','Date'],inplace=True)
data.head(5)| Date | ticker | Open | High | Low | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2010-01-04 | AAPL | 213.430 | 214.500 | 212.380 | 214.010 | 123432400.000 | 27.727 |
| 3 | 2010-01-05 | AAPL | 214.600 | 215.590 | 213.250 | 214.380 | 150476200.000 | 27.775 |
| 6 | 2010-01-06 | AAPL | 214.380 | 215.230 | 210.750 | 210.970 | 138040000.000 | 27.333 |
| 9 | 2010-01-07 | AAPL | 211.750 | 212.000 | 209.050 | 210.580 | 119282800.000 | 27.283 |
| 12 | 2010-01-08 | AAPL | 210.300 | 212.000 | 209.060 | 211.980 | 111902700.000 | 27.464 |
data['Date'] = pd.to_datetime(data['Date'].astype(str), format='%Y-%m-%d')
data.info()<class 'pandas.core.frame.DataFrame'>
Int64Index: 5412 entries, 0 to 5411
Data columns (total 8 columns):
Date 5412 non-null datetime64[ns]
ticker 5412 non-null object
Open 5412 non-null float64
High 5412 non-null float64
Low 5412 non-null float64
Close 5412 non-null float64
Volume 5412 non-null float64
Adj Close 5412 non-null float64
dtypes: datetime64[ns](1), float64(6), object(1)
memory usage: 380.5+ KB# if we only interested in adjusted close price, we can pivot the table
close_price = pd.pivot_table(data,index='Date',columns='ticker',values='Adj Close')close_price.head(6)| ticker | AAPL | INTC | MSFT |
|---|---|---|---|
| Date | |||
| 2010-01-04 | 27.727 | 16.443 | 25.555 |
| 2010-01-05 | 27.775 | 16.435 | 25.564 |
| 2010-01-06 | 27.333 | 16.380 | 25.407 |
| 2010-01-07 | 27.283 | 16.222 | 25.143 |
| 2010-01-08 | 27.464 | 16.403 | 25.316 |
| 2010-01-11 | 27.222 | 16.498 | 24.994 |
close_price.plot(figsize=(12,5))<matplotlib.axes._subplots.AxesSubplot at 0x7eff568117b8>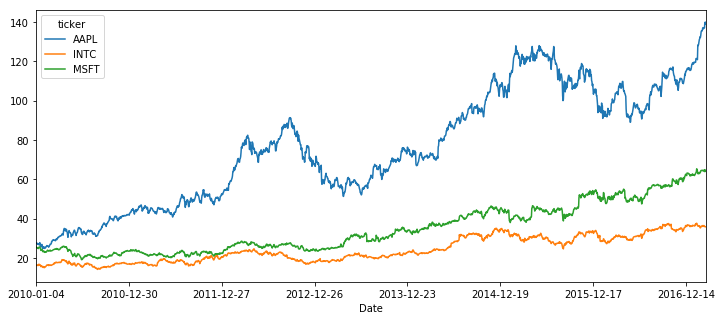
# if we want the return, Pandas provide an extremely easy transformation
stock_return = close_price.pct_change()
stock_return.head(5)| ticker | AAPL | INTC | MSFT |
|---|---|---|---|
| Date | |||
| 2010-01-04 | NaN | NaN | NaN |
| 2010-01-05 | 0.001729 | -0.000479 | 0.000323 |
| 2010-01-06 | -0.015906 | -0.003354 | -0.006137 |
| 2010-01-07 | -0.001849 | -0.009615 | -0.010400 |
| 2010-01-08 | 0.006648 | 0.011165 | 0.006897 |
#plot the cumulative return in one line
(1+stock_return).cumprod().plot()<matplotlib.axes._subplots.AxesSubplot at 0x7f76333135f8>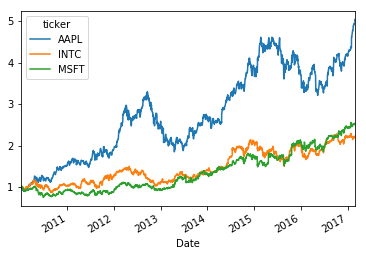
# just show the style of OOP
(1 + pd.pivot_table(data,index='Date',columns='ticker',values='Adj Close').pct_change()).cumprod().plot()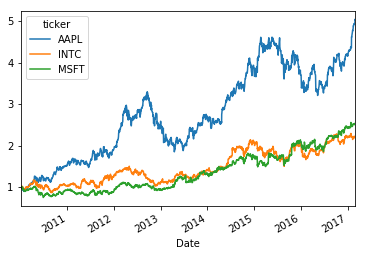
# save the return dataframe to csv
stock_return.to_csv('stockReturn.csv')# or, to save it to HDF5 format, which is much faster
# create a HDF store
hdf = pd.HDFStore('stock.h5')
hdf['stock_return'] = stock_return
hdf['raw_data'] = data
hdf.close()%timeit data = pd.read_csv('data.csv')100 loops, best of 3: 5.75 ms per loophdf = pd.HDFStore('stock.h5')
%timeit data = hdf['raw_data']The slowest run took 6.86 times longer than the fastest. This could mean that an intermediate result is being cached.
100 loops, best of 3: 2.61 ms per loop